Densely Connected Convolutional Networks. (CVPR 2017)
Authors: Gao Huang, Zhuang Liu, Laurens van der Maaten, Kilian Q. Weinberger.
- 본 논문에서는 ResNet으로 최근 네트워크의 깊이가 점점 깊어지지만, ResNet에서 발견된 문제인 많은 layer들이 실제로 많은 기여를 하지 못하고, training중 random하게 성능을 저하시키고, 또한 각 layer 별로 own weight를 가지기 때문에 파라미터의 수도 많다는 문제를 해결하기 위해 DenseNet을 제안한다.
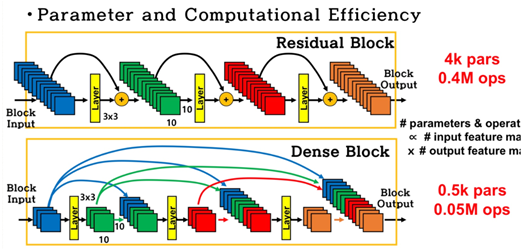
- DenseNet은 이전 layer들의 feature map을 다음 layer의 입력으로 연결하는 방식으로 ResNet이 feature map을 add했다면 DenseNet은 feature map을 concate하는 차이점을 가진다. 이러한 concat은 이전 feature map이 현재의 feature map과 서로 섞이지 않게 학습하게 만든다. 또한 연결을 통해 input feature와 middle layer의 feature가 지속적으로 네트워크에 연결되며 gradient vanishing 문제를 해결하고 feature propagation을 강화한다. 또한 parameter 수 또한 줄일 수 있다.
- Growth rate, 그림 2과 같이 이전 layer의 output을 계속 concat하면 channel이 계속해서 커져서 계산량이 늘어날 수 있다. 본 논문에서는growth rate라는 개념을 도입하여, 각 블록의 convolution들은 growth rate만큼만 channel을 output하여 channel의 수가 늘어나 계산량이 많아지는 문제를 해결한다.

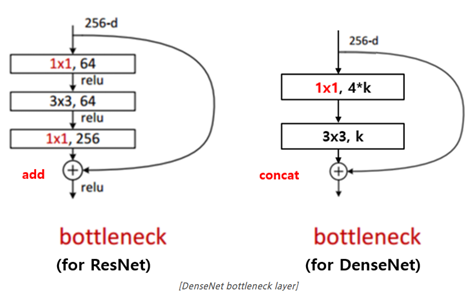
- Bottleneck layer, ResNet의 bottleneck block과 DensNet의 bottleneck block을 비교했을 때, 둘 다 3x3 convolution 이전에 1x1 convolution으로 feature map의 channel의 개수를 줄인다. ResNet은 이 후로 1x1 convolution을 통해 input feature map의 channel 개수만큼 늘리지만, DenseNet은 growth rate만큼 feature map을 생성한다는 차이가 있다. DenseNet은 1x1 convolution 연산으로 4*growth rate 개의 feature map을 만들고 3x3 convolution을 통해 growth rate개의 feature map으로 한번 더 줄인다. 이 bottleneck layer를 이용하면 동일한 파라미터 수를 이용했을 때 더 좋은 성능을 보였다.
- Transition block, DenseNet은 feature downsampling에 transition block을 사용한다. 이 block은 1x1 convolution과 2x2 average pooling으로 구성된다. 1x1 convolution 통해 feature map의 개수를 줄일 때 이 줄여주는 정도를 하이퍼 파라미터 theta를 이용하며 본 논문에서는 compression이라고 표현한다. 즉 transition layer에 들어가면 먼저 1x1 convolution에서 feature map의 개수가 theta를 통해 줄어들고, 2x2 average pooling으로 feature map의 width, height가 절반으로 줄어들게 된다. Theta=1일 경우 feature map의 개수를 줄이지 않고 그대로 가져오게 된다.




댓글